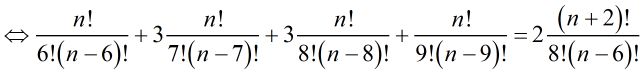Đề kiểm tra 15 phút – Chương 2 – Đề số 5 – Đại số và giải tích 11

 Xem những đề kiểm tra 15 p khác ở đây

Đề bài

Câu 1: Một thí sinh phải chọn 10 trong số 20 câu hỏi. Hỏi có bao nhiêu cách chọn 10 câu hỏi này nếu 3 câu đầu phải được chọn:

A. 

$C_{20}^{10}$

               B. 

$C_7^{10}+C_{10}^3$

C. 

$C_{10}^7.C_{10}^3$

       D. 

$C_{17}^7$

Câu 2: Giá trị của 

$n\in N$

 thỏa mãn đẳng thức 

$C_n^6+3C_n^7+3C_n^8+C_n^9=2C_{n+2}^8$

 là:

A. n = 18                     B. n = 16

C. n = 15                     D. n = 14

Câu 3: Trong các câu sau, câu nào sai:

A. 

$C_{14}^3=C_{14}^{11}$

                  

B. 

$C_{10}^3+C_{10}^4=C_{11}^4$

C. 

$C_4^0+C_4^1+C_4^2+C_4^3+C_4^4=16$

D. 

$C_{10}^4+C_{11}^4=C_{11}^5$

Câu 4: Nếu 

$A_x^2=110$

 thì

A. x =10

B. x = 11

C. x = 11 hay x = 10

D. x = 0

Câu 5: Trong mặt phẳng cho 2010 điểm phân biệt sao cho 3 điểm bất kỳ không thẳng hàng. Hỏi có bao nhiêu véc tơ khác véc tơ – không có điểm đầu và điểm cuối thuộc 2010 điểm đã cho.

A. 4039127                 B. 4038090

C. 4167114                 D. 167541284

Câu 6: Cho biết 

$C_n^{n-k}=28$

. Giá trị của n và k lần lượt là:

A. 8 và 4

B. 8 và 3

C. 8 và 2

D. Không thể tìm được

Câu 7: Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:

A. 11                           B. 10

C. 9                             D. 8

Câu 8: Nghiệm của phương trình 

$A_n^3=20n$

 là :

A. n = 6                       B. n = 5

C. n = 8                       D. Không tồn tại

Câu 9: Cho đa giác đều n đỉnh, 

$n\in N$

và 

$n\ge 3$

. Tìm n biết rằng đa giác đã cho có 135 đường chéo

A. n = 15                     B. n = 27

C. n = 8                       D. n = 18

Câu 10: Giải bất phương trình ( ẩn n thuộc tập tự nhiên ) 

$\frac{C_{n+1}^2}{C_n^2}\ge \frac{3}{10}n$

A. 

$2\le n<4$

   

B. 

$0\le n\le 2$

C. 

$1\le n\le 5$

D. 

$-\frac{2}{3}\le n\le 5$

Lời giải chi tiết

1D	2C	3D	4B	5B
6C	7A	8A	9D	10D

 

Câu 1:

Theo yêu cầu bài toán:

+ 3 câu đầu phải được chọn thì chỉ có 1 cách

+ Chọn 7 câu trong 17 câu còn lại có: 

$C_{17}^7$

 cách

Vậy có 

$C_{17}^7$

 cách.

Chọn đáp án D.

Câu 2:

Điều kiện: 

$n\ge 9$

Ta có: 

$C_n^6+3C_n^7+3C_n^8+C_n^9=2C_{n+2}^8$

Giải phương trình này có: 

$n=15$

Chọn đáp án C.

Câu 3:

Ta có: 

$\{\begin{array}{c}{C}_{10}^4+C_{11}^4=540\\ C_{11}^5=462\end{array}$$\Rightarrow C_{10}^4+C_{11}^4\ne C_{11}^5=462$

Chọn đáp án D.

Câu 4:

Điều kiện: 

$x\ge 2$

Ta có: 

$A_x^2=110\iff \frac{x!}{\left(x-2\right)!}=110$

$\iff x\left(x-1\right)=110\Rightarrow x=11$

Chọn B

Câu 5:

Số véc tơ khác véc tơ không có điểm đầu và điểm cuối thuộc 2010 điểm đã cho là 

$C_{2010}^2=4038090$

 (cách)

Chọn đáp án B.

Câu 6:

Ta có: 

$C_n^{n-k}=28\iff \frac{n!}{\left(n-k\right)!k!}=28$$\iff \{\begin{array}{c}n=8\\ k=2\end{array}$

Chọn đáp án C.

Câu 7:

Số đường chéo của đa giác được xác định bởi công thức

$\frac{n\left(n-3\right)}{2}$

=44${\displaystyle \frac{n\left(n-3\right)}{2}}=44$

$\iff n^2-3n-88=0$

$\iff [\begin{array}{c}n=11\end{array}$

n=−8

$\iff [\begin{array}{l}n=11\\ n=-8\end{array}$

Chọn đáp án A.

Câu 8:

Điều kiện: 

$n\ge 3$

Ta có: 

$A_n^3=20n\iff \frac{n!}{\left(n-3\right)!}=20n$

$\iff n\left(n-1\right)\left(n-2\right)=20n$

$\iff \left(n-1\right)\left(n-2\right)=20\iff [\begin{array}{c}n=6\end{array}$

n=−3

$\iff \left(n-1\right)\left(n-2\right)=20\iff [\begin{array}{l}n=6\\ n=-3\end{array}$

Chọn đáp án A.

Câu 9:

Số đường chéo của đa giác được xác định bằng công thức:

$\frac{n\left(n-3\right)}{2}$

=135${\displaystyle \frac{n\left(n-3\right)}{2}}=135$

$\iff n^2-3n-270=0$

$\iff [\begin{array}{c}n=18\end{array}$

n=−15

$\iff [\begin{array}{l}n=18\\ n=-15\end{array}$

Chọn đáp án D.

Câu 10:

Điều kiện: 

$n\ge 2$

Ta có: 

$\frac{C_{n+1}^2}{C_n^2}\ge \frac{3}{10}n$

$\iff \frac{\frac{\left(n+1\right)!}{2!\left(n-1\right)!}}{}$

n!2!(n−2)!

≥310

n$\iff {\displaystyle \frac{{\displaystyle \frac{\left(n+1\right)!}{2!\left(n-1\right)!}}}{{\displaystyle \frac{n!}{2!\left(n-2\right)!}}}}\ge {\displaystyle \frac{3}{10}}n$

$\iff \frac{n\left(n+1\right)}{n\left(n-1\right)}$

≥310

n$\iff {\displaystyle \frac{n\left(n+1\right)}{n\left(n-1\right)}}\ge {\displaystyle \frac{3}{10}}n$

$\iff \frac{n+1}{n-1}$

≥310

n$\iff {\displaystyle \frac{n+1}{n-1}}\ge {\displaystyle \frac{3}{10}}n$

$\iff 10n+10\ge 3n^2-3n$

$\iff 3n^2-13n-10\le 0$

$\iff -\frac{2}{3}$

≤n≤5$\iff -{\displaystyle \frac{2}{3}}\le n\le 5$

Chọn đáp án D