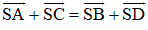Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 85: Cho hình tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu là A và điểm cuối là các điểm còn lại của hình tứ diện. Các vecto đó có cùng nằm trong một mặt phẳng không ?
Lời giải
Các vecto có điểm đầu là A và điểm cuối là các điểm còn lại của hình tứ diện là: AB→ , AC→ , AD→
Các vecto đó không cùng nằm trong một mặt phẳng
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 85: Cho hình hộp ABCD.A’B’C’D’. Hãy kể tên các vecto có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vecto AB
Lời giải
Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ AB→ là: DC→; A'B'→; D'C'→.
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 86: Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.3.2):
a)AB→ + CD→ + EF→ + GH→
b) BE→ - CH
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 89: Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vecto AF→, IK→ , ED→ đồng phẳng.
Lời giải
I và K lần lượt là trung điểm của các cạnh AB và BC ⇒ IK là đường trung bình của ∆ABC nên IK // AC ⊂ (AFC) ⇒ IK // (AFC)
hình hộp ABCD.EFGH nên các mặt của hình hộp là hình bình hành.
Suy ra: EF// CD(cùng // GH) và EF = CD ( cùng = GH)
EFCD là hình bình hành
⇒ ED // CF
Nên ED // (AFC)
⇒ ba vecto AF→, IK→, ED→ đồng phẳng (vì giá của chúng song song với một mặt phẳng)
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 89: Cho hai vecto a→ và b→ đều khác vecto 0→. Hãy xác định vecto c→ = 2a→ - b→ và giải thích tại sao ba vecto a→ , b→ , c→ đồng phẳng
Lời giải
→ ,b→ , c→ đồng phẳng vìa→ và b→ không cùng phương và có cặp số (2; -1)sao cho : c→ = 2a→ - b→
Trả lời câu hỏi Toán 11 Hình học Bài 1 trang 89: Cho ba vecto a→, b→ , c→ trong không gian. Chứng minh rằng nếu ma→ + nb→ + pc→ = 0→ và một trong ba số m, n, p khác không thì ba vecto a→, b→ , c→ đồng phẳng
Lời giải
Giả sử p ≠ 0 ta có:
Do đó, ba vecto a→ , b→ , c→ đồng phẳng theo định lí 1
Bài 1 (trang 91 SGK Hình học 11): Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Mặt phẳng (P) cắt các cạnh bên AA’, BB’, CC’, DD’ lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
a) Cùng phương với IA→;
b) Cùng hướng với IA→;
c) Ngược hướng với IA→.
Lời giải:
Bài 3 (trang 91 SGK Hình học 11): Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng (ABCD). Chứng minh rằng:
Lời giải:
Bài 4 (trang 92 SGK Hình học 11): Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng:
Bài 5 (trang 92 SGK Hình học 11): Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho :
Bài 6 (trang 92 SGK Hình học 11): Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABC. Chứng minh rằng
Lời giải:
Bài 7 (trang 92 SGK Hình học 11): Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng:
Bài 8 (trang 92 SGK Hình học 11): Cho lăng trụ tam giác ABC.A’B’C’ có AA'→=a→; AB→=b→; AC→=c→ . Hãy phân tích (hay biểu thị) các vectơ B'C→, BC'→ qua các vectơ a→ ,b→ , c→
Lời giải:
Bài 9 (trang 92 SGK Hình học 11): Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho và trên đoạn BC lấy điểm N sao cho . Chứng minh rằng ba vectơ , , đồng phẳng.
Lời giải:
Bài 10 (trang 92 SGK Hình học 11): Cho hình hộp ABCD.EFGH. Gọi K là giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba vectơ , , đồng phẳng.
Lời giải: